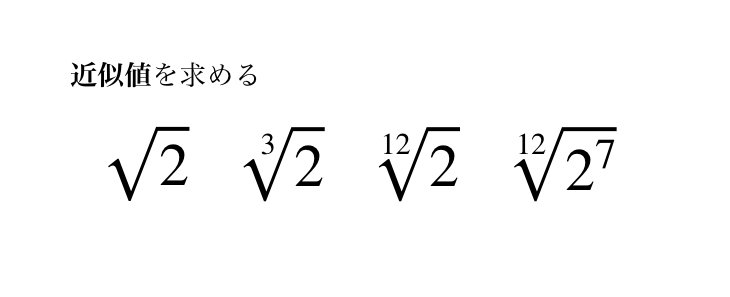2の12乗根(2の12じょうこん) は、代数的無理数である。音楽理論において非常に重要であり、十二平均律における半音の周波数比を表す。歴史的にこの数はシモン・ステヴィンによって1580年(草稿、1610年に書き直し)に調律との関連で初めて提唱された。
数値
有効数字20桁の2の12乗根は1.0594630943592952646である。正則連分数展開によるディオファントス近似は1, 17⁄16, 18⁄17, 89⁄84, 196⁄185, 1461⁄1379, 1657⁄1564, 3118⁄2943, 7893⁄7450, 18904⁄17843 ... である。
平均律の半音階
音程は周波数の比であるため、平均律の半音階はオクターブ(2:1の周波数比)を12等分する。
この値を中央ハ(C)の上のイ(A)音(440 Hzの周波数を持ち、A4と呼ばれる)から始まる半音階の音に連続的に適用することで、以下の音高列が得られる。
最後のA(A5: 880 Hz)は低い方のA(A4: 440 Hz)の厳密に2倍の周波数を持つ。つまり1オクターブ高い。
歴史
1636年にフランスの数学者マラン・メルセンヌによって計算された。
出典
推薦文献
- Barbour, J. M. (1933). “A Sixteenth Century Approximation for π”. American Mathematical Monthly 40 (2): 69–73. doi:10.2307/2300937. JSTOR 2300937.
- Ellis, Alexander; Helmholtz, Hermann (1954). On the Sensations of Tone. Dover Publications. ISBN 0-486-60753-4
- Partch, Harry (1974). Genesis of a Music. Da Capo Press. ISBN 0-306-80106-X
関連項目
- 純正律
- 音楽と数学
- 科学的ピッチ表記法
- 平均律クラヴィーア曲集
- 調律
- 冪根