大津の二値化法

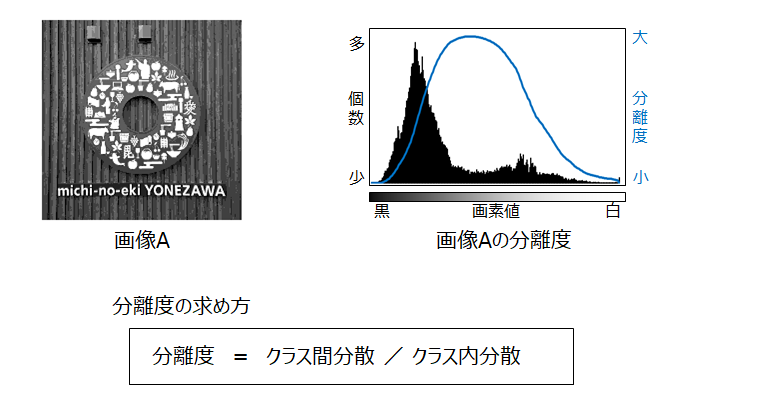
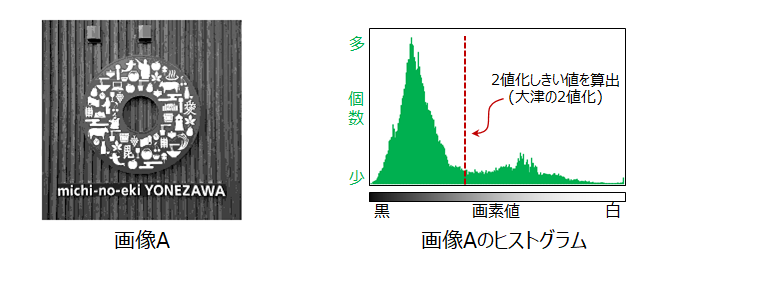
大津の二値化法（おおつのにちかほう、Otsu's method、大津の方法などとも呼ばれる）とは、コンピュータビジョンや画像処理において、自動画像しきい値処理を行うために使用される手法。その名は大津展之にちなむ。最も単純な形式では、アルゴリズムはピクセルをforegroundとbackgroundの2つのクラスに分ける1つの強度しきい値を返す。このしきい値はクラス内の強度分散を最小化することにより、または同等にクラス間の分散を最大化することにより決定される。

大津の二値化はフィッシャーの判別分析の1次元の離散に相当するものであり、ジェンクス最適化法に関連しており、強度ヒストグラムで行われる大域最適なK平均法と同等である。マルチレベルのしきい値処理へ拡大することは最初の論文で説明されており、以降計算効率の高い実装が提案されている。

大津の二値化

アルゴリズムは、2つのクラスの分散の加重和として定義されるクラス内分散を最小化するしきい値を探す。

${\displaystyle \sigma _{w}^{2}(t)=\omega _{0}(t)\sigma _{0}^{2}(t) \omega _{1}(t)\sigma _{1}^{2}(t)}$

加重${\displaystyle \omega _{0}}$と${\displaystyle \omega _{1}}$はしきい値${\displaystyle t}$により分けられた2つのクラスの確率であり、${\displaystyle \sigma _{0}^{2}}$と${\displaystyle \sigma _{1}^{2}}$はこれら2つのクラスの分散である。

クラスの確率${\displaystyle \omega _{0,1}(t)}$はヒストグラムの${\displaystyle L}$個のビンから計算される。

${\displaystyle {\begin{aligned}\omega _{0}(t)&=\sum _{i=0}^{t-1}p(i)\\[4pt]\omega _{1}(t)&=\sum _{i=t}^{L-1}p(i)\end{aligned}}}$

2つのクラスでは、クラス内分散を最小化することはクラス間分散を最大化することと同じである。

${\displaystyle {\begin{aligned}\sigma _{b}^{2}(t)&=\sigma ^{2}-\sigma _{w}^{2}(t)=\omega _{0}(t)(\mu _{0}-\mu _{T})^{2} \omega _{1}(t)(\mu _{1}-\mu _{T})^{2}\\&=\omega _{0}(t)\omega _{1}(t)\left[\mu _{0}(t)-\mu _{1}(t)\right]^{2}\end{aligned}}}$

これはクラス確率${\displaystyle \omega }$とクラス平均${\displaystyle \mu }$で表され、クラス平均${\displaystyle \mu _{0}(t)}$、${\displaystyle \mu _{1}(t)}$および${\displaystyle \mu _{T}}$は、

${\displaystyle {\begin{aligned}\mu _{0}(t)&={\frac {\sum _{i=0}^{t-1}ip(i)}{\omega _{0}(t)}}\\[4pt]\mu _{1}(t)&={\frac {\sum _{i=t}^{L-1}ip(i)}{\omega _{1}(t)}}\\\mu _{T}&=\sum _{i=0}^{L-1}ip(i)\end{aligned}}}$

である。以上の関係は以下のように簡単に確かめることができる。

${\displaystyle {\begin{aligned}\omega _{0}\mu _{0} \omega _{1}\mu _{1}&=\mu _{T}\\\omega _{0} \omega _{1}&=1\end{aligned}}}$

クラス確率とクラス平均は、繰り返し計算することができる。このアイデアは効果的なアルゴリズムを生む。

アルゴリズム

1. 各強度レベルのヒストグラムと確率を計算する。
2. ${\displaystyle \omega _{i}(0)}$と${\displaystyle \mu _{i}(0)}$の初期値を設定する。
3. ${\displaystyle t=1,\ldots }$ 最大強度までの全ての考えうるしきい値で次のステップを行う。
   1. ${\displaystyle \omega _{i}}$と${\displaystyle \mu _{i}}$を更新する。
   2. ${\displaystyle \sigma _{b}^{2}(t)}$を計算する。
4. 望ましいしきい値は${\displaystyle \sigma _{b}^{2}(t)}$が最大となる値である。

MATLABまたはOctaveでの実装

histogramCountsはさまざまなグレーレベルのグレースケール画像（通常は8ビット画像）の256画素のヒストグラムである。levelは画像のしきい値 (double) である。

MatlabにはImage Processing Toolboxに組み込み関数graythresh()とmultithresh()があり、それぞれ大津の手法とマルチ大津の手法(Multi Otsu's method)で実装されている。

Pythonでの実装

この実装にはNumPyライブラリが必要である

OpenCVやScikit-imageなどの画像処理専用のPythonライブラリは、アルゴリズムの組み込み実装を提案する。

限界とバリエーション

大津の方法は、ヒストグラムが2つのピークの間に深く鋭い谷を持つ二峰性分布を有するときにうまく機能する。

他の全ての大域的なしきい値処理と同様に、ノイズが大きく、対象のサイズが小さく、明暗が不均一で、クラス内の分散がクラス間の分散よりも大きい場合にパフォーマンスが低下する。このような場合、大津の方法を局所的に適用することが開発されている。

さらに、大津の方法の数学的根拠は、画像のヒストグラムを分散が等しくサイズが等しい2つの正規分布の混合としてモデル化する。しかし、大津のしきい値処理はこれらの仮定を満たさない場合でも満足のいく結果をもたらす可能性がある。同様に統計検定（大津の方法が密接に関連する）は、動作の仮定が完全に満たされていない場合でも正しく実行される。しかし、これらの仮定から生じる深刻な逸脱を無くすために、Kittler-Illingworthの方法などの大津の方法のいくつかのバリエーションが提案されている。

ノイズの多い画像に対するバリエーション

大津の方法の限界に対処するためにさまざまな拡張が開発されてきた。人気のある拡張の1つは、ノイズの多い画像のオブジェクトセグメンテーションのタスクに適した2次元大津の方法である。ここでは、特定のピクセルの強度値をそのすぐ近傍の平均強度と比較することでセグメンテーション結果を改良する。

各ピクセルで、近傍の平均グレーレベル値が計算される。与えられたピクセルのグレーレベルを${\displaystyle L}$個の離散値に分割し、平均グレーレベルも同じ${\displaystyle L}$個の値に分割する。その後、ピクセルのグレーレベルと近傍の平均のペア${\displaystyle (i,j)}$が形成される。各ペアは${\displaystyle L\times L}$個の考えうる2次元ビンの1つに属する。ペア${\displaystyle (i,j)}$の出現の総数（頻度）${\displaystyle f_{ij}}$を画像のピクセルの総数${\displaystyle N}$で割ったものは、2次元ヒストグラムで同時確率密度関数を定義する。

${\displaystyle P_{ij}={\frac {f_{ij}}{N}},\qquad \sum _{i=0}^{L-1}\sum _{j=0}^{L-1}P_{ij}=1}$

そして、2次元大津の方法は、2次元ヒストグラムに基づいて次のように開発されている。

2つのクラスの確率は、次のように表せる。

${\displaystyle {\begin{aligned}\omega _{0}&=\sum _{i=0}^{s-1}\sum _{j=0}^{t-1}P_{ij}\\\omega _{1}&=\sum _{i=s}^{L-1}\sum _{j=t}^{L-1}P_{ij}\end{aligned}}}$

2つのクラスの強度平均ベクトルと合計平均ベクトルは次のように表せる。

${\displaystyle {\begin{aligned}\mu _{0}&=[\mu _{0i},\mu _{0j}]^{T}=\left[\sum _{i=0}^{s-1}\sum _{j=0}^{t-1}i{\frac {P_{ij}}{\omega _{0}}},\sum _{i=0}^{s-1}\sum _{j=0}^{t-1}j{\frac {P_{ij}}{\omega _{0}}}\right]^{T}\\\mu _{1}&=[\mu _{1i},\mu _{1j}]^{T}=\left[\sum _{i=s}^{L-1}\sum _{j=t}^{L-1}i{\frac {P_{ij}}{\omega _{1}}},\sum _{i=s}^{L-1}\sum _{j=t}^{L-1}j{\frac {P_{ij}}{\omega _{1}}}\right]^{T}\\\mu _{T}&=[\mu _{Ti},\mu _{Tj}]^{T}=\left[\sum _{i=0}^{L-1}\sum _{j=0}^{L-1}iP_{ij},\sum _{i=0}^{L-1}\sum _{j=0}^{L-1}jP_{ij}\right]^{T}\end{aligned}}}$

ほとんどの場合、非対角の確率はわずかであるため、次のことを簡単に確認することができる。

${\displaystyle \omega _{0} \omega _{1}\cong 1}$

${\displaystyle \omega _{0}\mu _{0} \omega _{1}\mu _{1}\cong \mu _{T}}$

クラス間離散行列は次のように定義される。

${\displaystyle S_{b}=\sum _{k=0}^{1}\omega _{k}[(\mu _{k}-\mu _{T})(\mu _{k}-\mu _{T})^{T}]}$

離散行列のトレースは次のように表される。

${\displaystyle {\begin{aligned}&\operatorname {tr} (S_{b})\\[4pt]={}&\omega _{0}[(\mu _{0i}-\mu _{Ti})^{2} (\mu _{0j}-\mu _{Tj})^{2}] \omega _{1}[(\mu _{1i}-\mu _{Ti})^{2} (\mu _{1j}-\mu _{Tj})^{2}]\\[4pt]={}&{\frac {(\mu _{Ti}\omega _{0}-\mu _{i})^{2} (\mu _{Tj}\omega _{0}-\mu _{j})^{2}}{\omega _{0}(1-\omega _{0})}}\end{aligned}}}$

ここで

${\displaystyle \mu _{i}=\sum _{i=0}^{s-1}\sum _{j=0}^{t-1}iP_{ij}}$

${\displaystyle \mu _{j}=\sum _{i=0}^{s-1}\sum _{j=0}^{t-1}jP_{ij}}$

1次元の大津の方法と同様に、最適なしきい値${\displaystyle (s,t)}$は、${\displaystyle \operatorname {tr} (S_{b})}$を最大化することで取得される。

アルゴリズム

${\displaystyle s}$と${\displaystyle t}$は、1次元の大津の方法と同様に繰り返し取得される。${\displaystyle s}$と${\displaystyle t}$の値は、${\displaystyle \operatorname {tr} (S_{b})}$の最大値を取得するまで変更される。つまり、

${\displaystyle \operatorname {tr} (S_{b})}$を評価するために、高速再起動的プログラミングアルゴリズムを使用して時間パフォーマンスを向上させることができることに留意してください。しかし、動的プログラミングのアプローチを使用しても、2次元大津の方法は依然として時間計算量が非常に複雑である。したがって、計算コストを削減するために多くの研究が行われてきた。

合計領域テーブルを使用して3つのテーブルを作製する場合は、${\displaystyle P_{ij}}$を合計し、${\displaystyle i*P_{ij}}$を合計し、${\displaystyle j*P_{ij}}$を合計し、その時のランタイムの複雑性は(O(N_pixels), O(N_bins*N_bins))の最大値である。しきい値に関して粗い解像度のみが必要な場合はN_binsを減らすことができることに注意してください。

en:Summed-area table参照

Matlabでの実装

関数の入力と出力

histsは、グレースケール値と近傍平均グレースケール値のペアの${\displaystyle 256\times 256}$の2次元ヒストグラムである。

totalは、所与の画像のペアの数である。これは各方向の2次元ヒストグラムのビンの数により決まる。

thresholdは取得されたしきい値である。

不平衡な画像に対するバリエーション

画像のクラスのグレーレベルは正規分布とみなすことができるが、サイズや分散が等しくない場合、大津のアルゴリズムの仮定は満たされない。Kittler-Illingworthのアルゴリズム（最小エラーしきい値処理とも呼ばれる）はこのような場合を処理するための大津の方法のバリエーションである。このアルゴリズムを数学的に説明する方法はいくつかある。それらの1つは、試験される各しきい値について結果の2値画像の正規分布のパラメータがデータが与えられた最尤推定により推定されたことを考慮することである。

このアルゴリズムは大津の方法よりも優れているように見えることがあるが、推定される新しいパラメータが導入されるためアルゴリズムが過剰パラメータ化されて不安定になる可能性がある。大津の方法からの仮定が少なくとも部分的に有効であると考えられる多くの場合において、オッカムの剃刀に従ってKittler-Illingworthのアルゴリズムよりも大津の方法を優先する方が好ましい場合がある。

出典

外部リンク

• Implementation of Otsu's thresholding method as GIMP-plugin using Script-Fu (a Scheme-based language)
• Lecture notes on thresholding – covers the Otsu method
• A plugin for ImageJ using Otsu's method to do the threshold
• A full explanation of Otsu's method with a working example and Java implementation
• Implementation of Otsu's method in ITK
• Otsu Thresholding in C# – a straightforward C# implementation with explanation
• Otsu's method using MATLAB
• Otsu Thresholding with scikit-image in Python