量子テレポーテーション（りょうしテレポーテーション、英:Quantum teleportation）とは、量子状態を転送する技術である。古典的な情報伝達手段と量子もつれ (Quantum entanglement) の効果を複合的に利用して行われる。

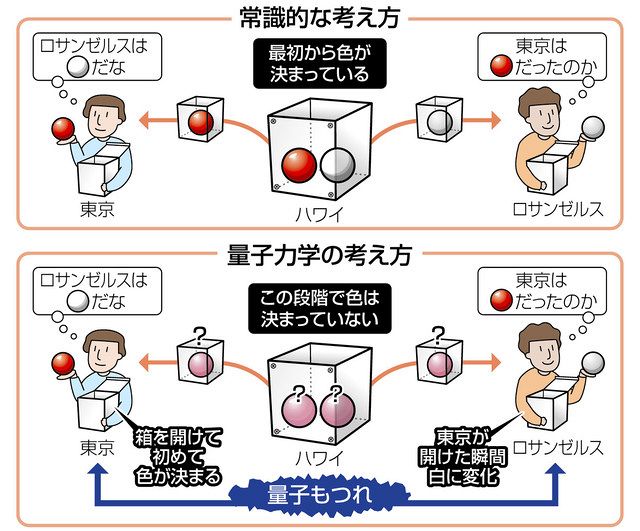
テレポーテーションという名前であるものの、ある量子状態の粒子が空間の別の場所に瞬間移動することを意味するのではない。量子テレポーテーションで利用される、「量子もつれの関係にある2つの粒子のうち一方の状態を観測すると、観測と同時に離れた位置にあるもう一方の粒子の状態が確定する」という量子力学における非局所性とよばれる性質に関連してこのような名前がついた。

古典的な情報転送経路が俗に古典チャンネルと呼ばれることに対し、量子もつれによる転送を、EPR相関に由来して、アインシュタイン＝ポドルスキー＝ローゼン (Einstein-Podolsky-Rosen; EPR) チャンネルと呼ぶ。古典チャンネルのみで任意の混合状態を含む量子状態を送信することは不可能であり、そのような量子状態の送信には系自体を送信するか、古典チャンネルとEPRチャンネルを組み合わせて利用する量子テレポーテーションを用いる必要がある。

原理

量子テレポーテーションはEPRペアという量子もつれの関係にある2つの粒子を用いる。例として最も簡単な光子の偏光の場合(1量子ビットの転送)について説明する。ここで、 | V ⟩ 0 {\displaystyle |V\rangle _{0}} は光子0の垂直偏光状態、 | H ⟩ 0 {\displaystyle |H\rangle _{0}} は光子0の水平偏光状態を表すものとする。 | ψ ⟩ 0 {\displaystyle |\psi \rangle _{0}} を光子0の偏光に関する量子状態とすると、そのような状態は常に

| ψ ⟩ 0 = α | V ⟩ 0 β | H ⟩ 0 {\displaystyle |\psi \rangle _{0}=\alpha |V\rangle _{0} \beta |H\rangle _{0}}

という形に表される。 α および β は重ね合わせの係数である。

ある光子1と光子2がEPRペアとして以下のような量子もつれの関係にあるとする。 | Φ ⟩ = 1 2 ( | V ⟩ 1 | V ⟩ 2 | H ⟩ 1 | H ⟩ 2 ) {\displaystyle |\Phi ^{ }\rangle ={\frac {1}{\sqrt {2}}}(|V\rangle _{1}|V\rangle _{2} |H\rangle _{1}|H\rangle _{2})}

この式には、光子1と光子2の偏光状態が平行しているという意味が含まれている。すなわち、一方の光子で水平偏光が観測されたならば、もう一方の光子も観測の有無にかかわらず水平偏光であることが確定し、逆もしかり、一方が観測により垂直偏光であったなら、もう一方も垂直偏光であることが未観測のまま確定する。

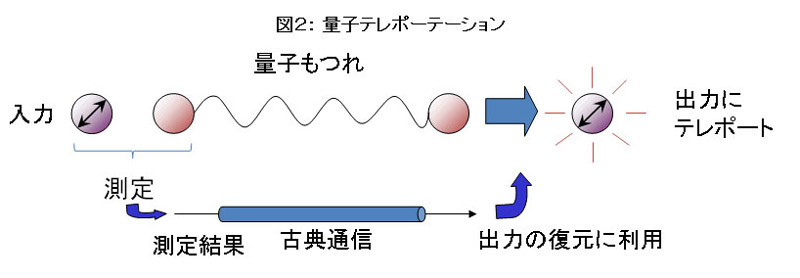
量子テレポーテーションの一例として、AさんからBさんにある光子0の量子状態 | ψ ⟩ 0 {\displaystyle |\psi \rangle _{0}} (1量子ビット)を量子テレポーテーションによって転送する場合を考える。

まずAさんは光子0とは別に事前に上記のEPRペアの光子２つ（光子1、光子2）を生成し光子2をBさんに送っておく。次に、Aさんは光子1を送信したい量子状態 | ψ ⟩ 0 {\displaystyle |\psi \rangle _{0}} にある光子0とあわせて特殊な観測（ベル測定）を行う。その観測結果を古典的な情報転送によってBさんに知らせれば、Bさんはその情報に基づいて手元の光子2に特定の操作をすることで、目的の量子状態 | ψ ⟩ 0 {\displaystyle |\psi \rangle _{0}} を光子2に再現することができる。

以下では簡単のため、 | V ⟩ , | H ⟩ {\displaystyle |V\rangle ,|H\rangle } を | 0 ⟩ , | 1 ⟩ {\displaystyle |0\rangle ,|1\rangle } と表記する。

ベル測定とは、ベル基底への射影測定を指す。今回の場合、特定の光子の状態は水平偏光か垂直偏光かという2つの区別された状態の重ね合わせであり、そのような量子系は2準位系と呼ばれ、２準位系のベル基底は次の4つとなる。

| Φ ⟩ = 1 2 ( | 00 ⟩ | 11 ⟩ ) {\displaystyle |\Phi ^{ }\rangle ={\frac {1}{\sqrt {2}}}(|00\rangle |11\rangle )} ,
| Φ − ⟩ = 1 2 ( | 00 ⟩ − | 11 ⟩ ) {\displaystyle |\Phi ^{-}\rangle ={\frac {1}{\sqrt {2}}}(|00\rangle -|11\rangle )} ,
| Ψ ⟩ = 1 2 ( | 01 ⟩ | 10 ⟩ ) {\displaystyle |\Psi ^{ }\rangle ={\frac {1}{\sqrt {2}}}(|01\rangle |10\rangle )} ,
| Ψ − ⟩ = 1 2 ( | 01 ⟩ − | 10 ⟩ ) {\displaystyle |\Psi ^{-}\rangle ={\frac {1}{\sqrt {2}}}(|01\rangle -|10\rangle )} .


初期の3つの光子の状態は次の状態ベクトルで表される。

| ψ ⟩ 0 ⊗ | Φ ⟩ 12 = ( α | 0 ⟩ 0 β | 1 ⟩ 0 ) ⊗ 1 2 ( | 0 ⟩ 1 ⊗ | 0 ⟩ 2 | 1 ⟩ 1 ⊗ | 1 ⟩ 2 ) . {\displaystyle |\psi \rangle _{0}\otimes |\Phi ^{ }\rangle _{12}=(\alpha |0\rangle _{0} \beta |1\rangle _{0})\otimes {\frac {1}{\sqrt {2}}}(|0\rangle _{1}\otimes |0\rangle _{2} |1\rangle _{1}\otimes |1\rangle _{2}).}

ベル基底を使って01を表すと、

| 0 ⟩ ⊗ | 0 ⟩ = 1 2 ( | Φ ⟩ | Φ − ⟩ ) , {\displaystyle |0\rangle \otimes |0\rangle ={\frac {1}{\sqrt {2}}}(|\Phi ^{ }\rangle |\Phi ^{-}\rangle ),}
| 0 ⟩ ⊗ | 1 ⟩ = 1 2 ( | Ψ ⟩ | Ψ − ⟩ ) , {\displaystyle |0\rangle \otimes |1\rangle ={\frac {1}{\sqrt {2}}}(|\Psi ^{ }\rangle |\Psi ^{-}\rangle ),}
| 1 ⟩ ⊗ | 0 ⟩ = 1 2 ( | Ψ ⟩ − | Ψ − ⟩ ) , {\displaystyle |1\rangle \otimes |0\rangle ={\frac {1}{\sqrt {2}}}(|\Psi ^{ }\rangle -|\Psi ^{-}\rangle ),}
| 1 ⟩ ⊗ | 1 ⟩ = 1 2 ( | Φ ⟩ − | Φ − ⟩ ) . {\displaystyle |1\rangle \otimes |1\rangle ={\frac {1}{\sqrt {2}}}(|\Phi ^{ }\rangle -|\Phi ^{-}\rangle ).}

となるので、これらを代入すると次のようになる。

| ψ ⟩ 0 ⊗ | Φ ⟩ 12 = 1 2 [ | Φ ⟩ 01 ⊗ ( α | 0 ⟩ 2 β | 1 ⟩ 2 ) | Φ − ⟩ 01 ⊗ ( α | 0 ⟩ 2 − β | 1 ⟩ 2 ) | Ψ ⟩ 01 ⊗ ( β | 0 ⟩ 2 α | 1 ⟩ 2 ) | Ψ − ⟩ 01 ⊗ ( − β | 0 ⟩ 2 α | 1 ⟩ 2 ) ] . {\displaystyle {\begin{aligned}|\psi \rangle _{0}\otimes |\Phi ^{ }\rangle _{12}={\frac {1}{2}}{\Big [}&|\Phi ^{ }\rangle _{01}\otimes (\alpha |0\rangle _{2} \beta |1\rangle _{2}) |\Phi ^{-}\rangle _{01}\otimes (\alpha |0\rangle _{2}-\beta |1\rangle _{2})\\&|\Psi ^{ }\rangle _{01}\otimes (\beta |0\rangle _{2} \alpha |1\rangle _{2}) |\Psi ^{-}\rangle _{01}\otimes (-\beta |0\rangle _{2} \alpha |1\rangle _{2}){\Big ]}.\end{aligned}}}

上式より、この状態にある三つの光子のうち光子0,1に対してベル測定を行えば、ベル基底の四つのうちいずれかとなる測定結果に応じて、光子2の状態が次の4つのいずれかに確定するとわかる。

α | 0 ⟩ 2 β | 1 ⟩ 2 {\displaystyle \alpha |0\rangle _{2} \beta |1\rangle _{2}}
α | 0 ⟩ 2 − β | 1 ⟩ 2 {\displaystyle \alpha |0\rangle _{2}-\beta |1\rangle _{2}}
β | 0 ⟩ 2 α | 1 ⟩ 2 {\displaystyle \beta |0\rangle _{2} \alpha |1\rangle _{2}}
− β | 0 ⟩ 2 α | 1 ⟩ 2 {\displaystyle -\beta |0\rangle _{2} \alpha |1\rangle _{2}}

ここでAさんはBさんにベル測定の結果を伝え(古典チャンネル)、BさんはAさんから伝えられた測定結果に応じて、上記のいずれか一つに状態が確定している光子2に対し次にようなパウリ演算子をそれぞれ行う。

  • | Φ ⟩ 01 {\displaystyle |\Phi ^{ }\rangle _{01}} の場合は何も行わない。
  • | Φ − ⟩ 01 {\displaystyle |\Phi ^{-}\rangle _{01}} の場合 σ z = [ 1 0 0 − 1 ] {\displaystyle \sigma _{z}={\begin{bmatrix}1&0\\0&-1\end{bmatrix}}}
  • | Ψ ⟩ 01 {\displaystyle |\Psi ^{ }\rangle _{01}} の場合 σ x = [ 0 1 1 0 ] {\displaystyle \sigma _{x}={\begin{bmatrix}0&1\\1&0\end{bmatrix}}}
  • | Ψ − ⟩ 01 {\displaystyle |\Psi ^{-}\rangle _{01}} の場合 σ z σ x = i σ y = [ 0 1 − 1 0 ] . {\displaystyle \sigma _{z}\sigma _{x}=i\sigma _{y}={\begin{bmatrix}0&1\\-1&0\end{bmatrix}}.}

すると、最終的なBさんの持つ光子2の状態は α | 0 ⟩ 2 β | 1 ⟩ 2 {\displaystyle \alpha |0\rangle _{2} \beta |1\rangle _{2}} となり、転送したかった光子0の量子状態を完全に再現できる。

ベル測定を行ったことで、元の光子0の量子状態は消滅してしまったが、光子2に突如として現れたように見える。

このように、あたかも"突如として遠隔地にふっと湧いてでる"ように感じられるのが、量子"テレポーテーション"というネーミングの由来である。

実験

量子テレポーテーション技術の詳細な論文は、チャールズ・ベネットらによって1993年に発表された。

長い間、実験は困難であるとされてきたが、1997年にアントン・ツァイリンガー率いるインスブルック大学（およびローマ大学）のグループのD. Bouwmeesterが初めて（離散変数の）量子テレポーテーション実験を成功させた。しかしながら、彼らの実験はある条件を満たすときだけテレポーテーションが起こるものであった。このため、ベネットが示した本当の意味でのテレポーテーションには成功していないと批判する論文もあり、彼らもその欠点について認めている。翌1998年、インスブルック大学と量子テレポーテーション実験で競争をしていたカリフォルニア工科大学のH. Jeff Kimble率いるグループの古澤明は、無条件の量子テレポーテーション（連続変数の量子テレポーテーション）に成功した。

2004年には、古澤明らが3者間での量子テレポーテーション実験を成功させた。さらに2009年には9者間での量子テレポーテーション実験を成功させた。これらの実験の成功により、量子を用いたネットワークを構成できることが実証された。

2013年8月、古澤明東大工学部教授を中心とするグループが、完全な量子テレポーテーションに成功した。波の性質の転送技術を改良し、従来の100倍となる61％の成功率であった。

2016年8月16日、中華人民共和国の研究チームが世界初の量子通信衛星を打ち上げた。また、同年8月26日には地上と宇宙間の量子通信試験に世界で初めて成功した。

2017年7月、国立研究開発法人情報通信研究機構が地上と宇宙の量子通信に超小型衛星としては世界で初めて成功した。この通信は、茨城県つくば市の民間企業が開発した衛星「SOCRATES」と情報通信研究機構の地上基地局との600km間で行われ、量子通信がより低コストな小型衛星で実現できることを実証した。


2021年5月、理化学研究所創発物性科学研究センター、シドニー大学、ルール大学ボーフムの共同研究チームは、確率的テレポーテーションに成功した。

脚注

参考文献

  • Bennett, Charles H.; Brassard, Gilles; Crépeau, Claude; Jozsa, Richard; Peres, Asher; Wootters, William K. (Mar 1993). “Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels”. Phys. Rev. Lett. 70 (13): 1895–1899. doi:10.1103/PhysRevLett.70.1895. http://link.aps.org/doi/10.1103/PhysRevLett.70.1895. 
  • Braunstein, Samuel L.; Kimble, H. J. (1998年8月27日). “A posteriori teleportation”. Nature 394 (6696): 840–841. doi:10.1038/29674. ISSN 0028-0836. https://doi.org/10.1038/29674. 
  • Bouwmeester, Dik; Pan, Jian-Wei; Mattle, Klaus; Eibl, Manfred; Weinfurter, Harald; Zeilinger, Anton (1997年12月11日). “Experimental quantum teleportation”. Nature 390 (6660): 575–579. doi:10.1038/37539. ISSN 0028-0836. https://doi.org/10.10380/37539. 
  • Furusawa, A.; Sørensen, J. L.; Braunstein, S. L.; Fuchs, C. A.; Kimble, H. J.; Polzik, E. S. (1998). “Unconditional Quantum Teleportation”. Science 282 (5389): 706–709. doi:10.1126/science.282.5389.706. ISSN 0036-8075. http://science.sciencemag.org/content/282/5389/706. 
  • Takeda, Shuntaro; Mizuta, Takahiro; Fuwa, Maria; van Loock, Peter; Furusawa, Akira (2013年8月15日). “Deterministic quantum teleportation of photonic quantum bits by a hybrid technique”. Nature 500 (7462): 315–318. arXiv:1402.4895. doi:10.1038/nature12366. ISSN 0028-0836. 
  • H. Yonezawa, T. Aoki, and A. Furusawa, Demonstration of a quantum teleportation network for continuous variables, Nature Vol. 431, pp.430-433 (2004)
  • 平野琢也「量子テレポーテーション」『OplusE』第27巻第6号、2005年、655-659頁。 

関連項目

  • 瞬間移動
  • 量子力学
    • 不確定性原理
    • 量子暗号
    • 量子コンピュータ
    • 量子もつれ

量子テレポーテーション YouTube

ノーベル物理学賞「量子もつれ」とは アインシュタインが「不気味」 奇妙な性質がもたらす未来：東京新聞デジタル

NTTと阪大、“テレポーテーション型”の量子計算を世界で初めて実証 2枚目の写真・画像 RBB TODAY

テレポーテーションと量子状態/量子チャンネルの双対性 物理とか

量子テレポーテーション YouTube