赤方偏移

赤方偏移（せきほうへんい、英: redshift）とは、主に天文学において、遠方の天体から到来する電磁波の波長が、ドップラー効果によって長くなる（可視光で言うと赤くなる）現象をいう。

赤方偏移による波長のずれは、天体の光を分光し、フラウンホーファー線を観察することによって調べることができる。波長λのスペクトルがΔλだけずれている場合、赤方偏移の量 z を

${\displaystyle z={\frac {\Delta \lambda }{\lambda }}}$

と定義する。

観測可能なほぼ全ての銀河の光に赤方偏移が見られることから、宇宙が膨張していることを示す証拠であると考えられている。

概要

光のドップラー効果

遠ざかる音源からの音がドップラー効果により低くなるのと同様、遠ざかる光源から発せられた光には赤方偏移がおこる。例えば、地球に対して遠ざかるような運動をしている恒星のスペクトルを測定すると、地球から見た視線方向の後退速度に対応する赤方偏移が観測される。静止系で波長λの光が観測者に向かってvで運動するとき、観測者から見た光の波長λ'は

　${\displaystyle \lambda '=\lambda {\sqrt {\frac {c-v}{c v}}}}$

で与えられる。ただしcは光速で、${\displaystyle |v|$ である。

宇宙論的赤方偏移

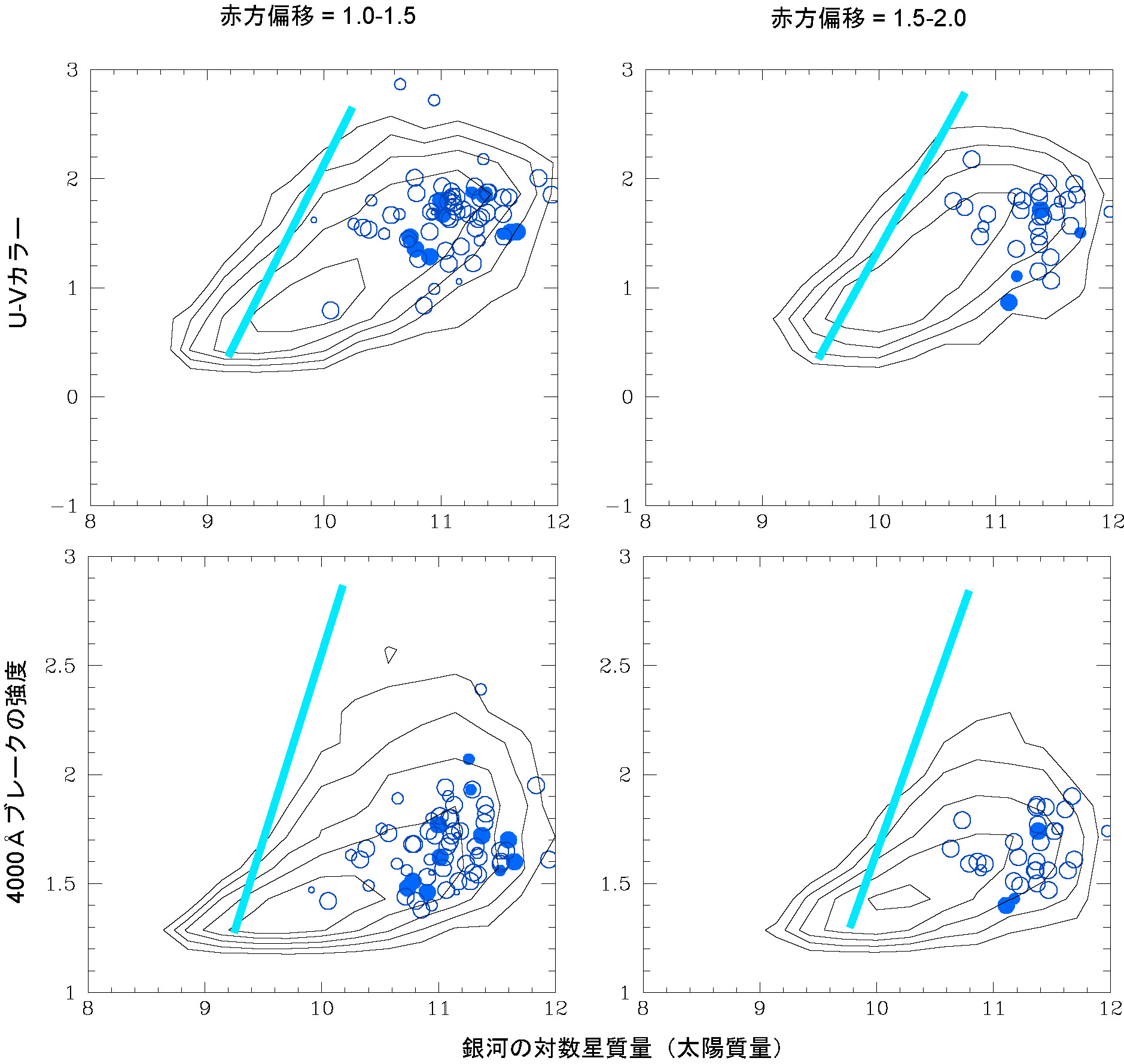
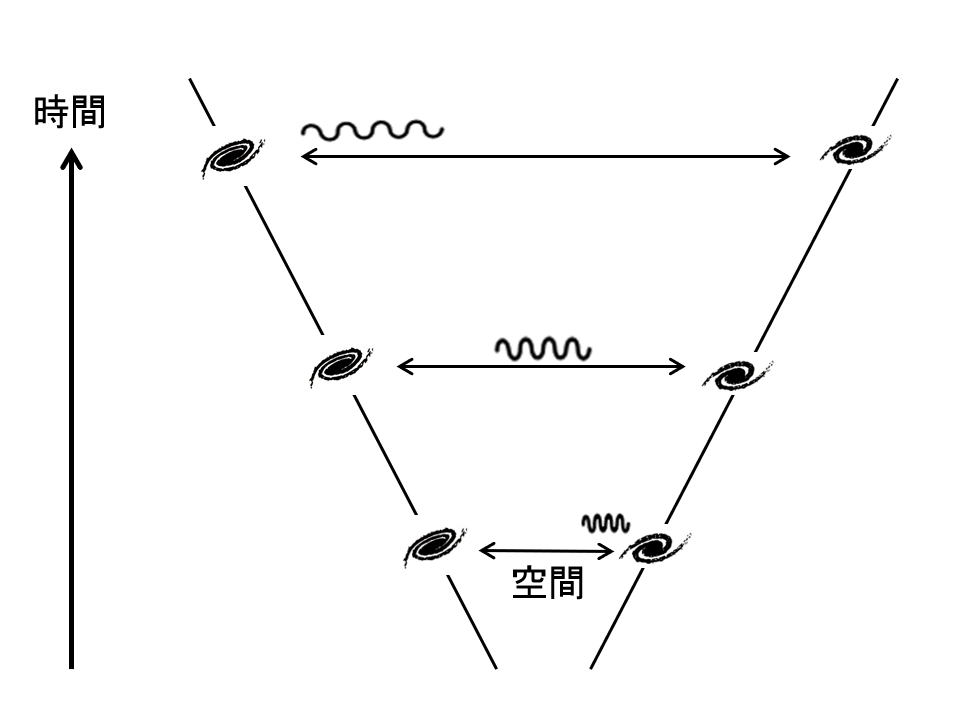
アメリカ合衆国の天文学者エドウィン・ハッブルは、様々な銀河までの距離とその銀河のスペクトルを調べ、ほとんど全ての銀河のスペクトルに赤方偏移が見られること、赤方偏移の量は遠方の銀河ほど大きいことを発見した（ハッブルの法則）。この事象は、銀河を出た光が地球に届くまでの間に空間自体が伸びて波長が引き伸ばされるためであると解釈でき、宇宙が膨張していることを示すと考えられている。2020年現在、観測されている最も z が大きい（すなわち最も遠方にあると考えられる）天体は z = 10.957 の銀河 GN-z11 である。また、HD1 は2022年4月時点で、観測可能な宇宙において地球から最も遠い距離に位置している可能性がある既知の天体として知られている。

もう一つの代表的な例として、宇宙背景放射での現象が挙げられる。現在の宇宙では、絶対温度約 3K の黒体放射に相当する放射があらゆる方向からやってきており、宇宙背景放射と呼ばれている。これは、宇宙創成期に宇宙を満たしていた高温状態のプラズマから発せられた熱放射が、ビッグバン後の急激な宇宙の膨張によって波長が引き伸ばされて極端な赤方偏移を受け、現在観測されるような電磁波(特に、マイクロ波)として観測されているものである。これは現在知られている最大の赤方偏移であり、 z = 1089 （距離換算で約138.12億光年）である。

重力赤方偏移

重力赤方偏移（gravitational redshift）とは、重力場中の光の波長が長くなる現象である。

一般相対性理論において、時間の流れがどれくらい変化するかは、計量という式によって表わされる。最も簡単なシュヴァルツシルトの解では、質量Mの天体から距離rだけ離れた地点における計量は以下の式になる。

${\displaystyle \Delta \tau ={\sqrt {1-{\frac {2GM}{c^{2}r}}}}\Delta t}$

ここで、${\displaystyle \Delta \tau }$は、距離rの地点における時間の流れを表わし、${\displaystyle \Delta t}$はその天体から無限遠方の地点における時間の流れを表わす。この式により、距離rの地点における時間の流れが遅くなることが表わされる。また、${\displaystyle 2GM/c^{2}}$はシュヴァルツシルト半径を表しており、距離rがシュヴァルツシルト半径に等しいときは遠方からは時間が全く経過しないように見えることを示している。

光の波長λ、振動数νと光速度cとの間には、λν = c の関係がある。光の振動数は単位時間当たりの振動の回数であるから、時間の進み方が遅くなると遠方の観測者からは、振動数は小さく、波長は長く観測される。

これを使って、重力赤方偏移の大きさを計算すると以下のようになる。天体の中心から距離rの地点で波長${\displaystyle \lambda _{\mathrm {em} }}$の光が放射され、遠く離れた地点において、その光の波長が${\displaystyle \lambda _{\mathrm {rec} }}$と観測されたとすると、

${\displaystyle \lambda _{\mathrm {em} }={\sqrt {-g_{tt}}}\lambda _{\mathrm {rec} }={\sqrt {1-{\frac {2GM}{c^{2}r}}}}\lambda _{\mathrm {rec} }}$

この${\displaystyle \lambda _{\mathrm {em} }}$を、赤方偏移zの定義、

${\displaystyle z={\frac {\lambda _{\mathrm {rec} }-\lambda _{\mathrm {em} }}{\lambda _{\mathrm {em} }}}}$

に代入すると、zの式は${\displaystyle \lambda _{\mathrm {rec} }}$の式となる。すなわち、zの理論上の値が、観測値${\displaystyle \lambda _{\mathrm {rec} }}$から計算できる。

1984年、宇宙科学研究所（ISAS）のX線観測衛星 てんま が、中性子星の強い重力による重力赤方偏移を世界で初めて捉えたと報じた。

赤方偏移を扱った作品

• 『バーサーカー』シリーズ（フレッド・セイバーヘーゲン）
• 時の果てのフェブラリー ─赤方偏移世界─（山本弘）
• 青い宇宙の冒険（小松左京）
• 時間に挟まれた男（ロバート・シェクリイ）
• おねがい☆ティーチャー、おねがい☆チュータ（時間停止（仮死）状態になる「停滞」患者の外見の特徴としての、「瞳の色」として設定された）

出典

関連項目

• 青方偏移
• エドウィン・ハッブル